Gameboy Genius

Interesting question, if 1=5, 2=10, 3=15, 4=20… what is 5=? (Trolling with maths)

November 13th, 2012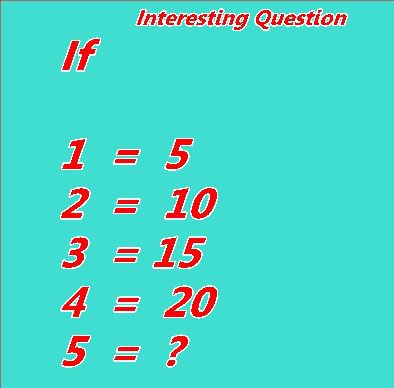

This image has been going around Facebook lately. What is the answer?

You might be rushing to say obviously 25! You might solve the equation and get this answer. But if you’re a bit of a smart-ass you might be thinking, hey wait a minute, those are equals signs! The answer is obviously 1! It says so on the first line. If 1=5, then surely 5=1. If you’re even more of a smart-ass you might point out that the 1-5 on the left side could be symbols, (much like x or y) and that the value of the symbol 5 could be anything.

However, let’s pretend that the correct interpretation is that you put the left side into some function f(x), such that you get the value on the right side.

f(1) = 5
f(2) = 10
f(3) = 15
f(4) = 20
f(5) = ?

The obvious candidate would be f(x) = 5x, in other words to multiply the number on the left side by 5, which would give f(5)=25.

That’s boring. Can we construct a function such that the first four lines still hold true, while f(5) takes on any arbitrary value? The answer is yes. You might remember from math class that you can solve a polynomial equation by moving everything to one side so you have (some polynomial) = 0 and then factoring the polynomial.
x³ - 6x² + 5x = -12
could also be factored and written as
(3-x)(4-x)(1+x) = 0
You can confirm this by expanding the latter expression and realize that the fully expanded form matches the former expression. The latter form has an advantage when solving the equation because = 0 puts a constraint on the left side: anything multiplied by zero equals zero. For this reason, we know that for example when 3-x = 0, the whole expression on the left side equals zero. We can see that if x = 3, the whole expression becomes
(3-3)(4-3)(1+3) = 0*1*4 = 0
and we can conclude that since we have equality, x=3 is one of the roots for the equation.

Enough with the repetition of high school maths. How does this help us create a function that can give us an arbitrary value for f(5)? Well, let’s begin by crafting a function that returns 0 for all the values involved:
f(x) = (x-1)(x-2)(x-3)(x-4)(x-5)
Like before, if x = 3, then x-3 = 0 and the whole expression is zeroed out. It will still have all sorts of values for values of x other than our list of integers, 1 to 5. f(2.5) = 1.40625 for example, but we don’t care about that, for our purposes, do we?
We now have:

f(1) = 0
f(2) = 0
f(3) = 0
f(4) = 0
f(5) = 0

Here’s the graph for good measure, even though we don’t care about what the function does for other values.

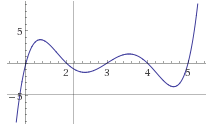
Pretty neat. We can now remove one term from this multiplication, say x-1 so you get f(x) = (x-2)(x-3)(x-4)(x-5) 2 to 5 will still be “zeroed” like before, whereas 1 will now have a non-zero value.

f(1) = 24
f(2) = 0
f(3) = 0
f(4) = 0
f(5) = 0

A similar expression could be created by removing the (x-2) part from the original expression: f(x) = (x-1)(x-3)(x-4)(x-5)

f(1) = 0
f(2) = -6
f(3) = 0
f(4) = 0
f(5) = 0

And so on with each term of the multiplication…
The important thing to realize, is that you can add these expressions together and use each expression to single out one of the integers in the range, and modify its value. You do this by multiplying one of the sub-expressions by any suitable value. Since any of the sub-expressions will only have a non-zero value when x equals a particular value in the list.
So let’s try out our new super powers.

f(x) = (2-x)(3-x)(4-x)(5-x) +
(1-x)(3-x)(4-x)(5-x) +
(1-x)(2-x)(4-x)(5-x) +
(1-x)(2-x)(3-x)(5-x) +
(1-x)(2-x)(3-x)(4-x)

f(1) = 24
f(2) = -6
f(3) = 4
f(4) = -6
f(5) = 24

Now you can normalize each sub-expression by dividing it with output of that expression for that value x.

f(x) = (2-x)(3-x)(4-x)(5-x)/24 +
(1-x)(3-x)(4-x)(5-x)/-6 +
(1-x)(2-x)(4-x)(5-x)/4 +
(1-x)(2-x)(3-x)(5-x)/-6 +
(1-x)(2-x)(3-x)(4-x)/24

f(1) = 1
f(2) = 1
f(3) = 1
f(4) = 1
f(5) = 1

Now you can multiply each sub-expression by the value you want the function to return for the corresponding value of x.

f(x) = 5 * (2-x)(3-x)(4-x)(5-x)/24 +
10 * (1-x)(3-x)(4-x)(5-x)/-6 +
15 * (1-x)(2-x)(4-x)(5-x)/4 +
20 * (1-x)(2-x)(3-x)(5-x)/-6 +
42 * (1-x)(2-x)(3-x)(4-x)/24

f(1) = 5
f(2) = 10
f(3) = 15
f(4) = 20
f(5) = 42

Now you can claim that the number series in the image actually represents this particular function you just created and that the correct answer for “5 =” is whatever you want it to be.

Boredom -> trolling with maths in ways no one gives a shit about.